今回は統計の基本的な部分となる基本統計量を扱ってみます。統計、というと小難しい印象を受けてしまいますが、基本的な部分は馴染みが合ってすぐに理解可能ですし実践も容易です。統計は、大別すると「推測統計」と「記述統計」に別れます。推測統計は、限られた標本から母集団のデータの特長を推測します。記述統計は、データの特徴をグラフや表で簡単にわかりやすく表現します。統計を用いるときは本丸としては推測統計なのですが、こちらは難易度が上がりますので、基本的な部分である記述統計の中の基本統計量にスポットをあてます。
基本統計量は、データの基本的な特性を表すものです。この説明だけだとわかりにくいですので解説を少し加えます。例えば売上のデータが100件あるとして、平均値という基本統計量を知りたいとします。平均は皆様が一番馴染みのある統計量なので例として挙げました。売上データを100件全部を並べてみて、売上の真ん中らへんは大体ここらへんかな、と勘で当たりをつける方はいないと思います。売上データを全部足して100件で割る。そうすると、平均値という基本的な特性を知ることができます。これを難しくいうと「基本統計量」となります。(更に厳密にいうとこの平均は算術平均と呼びます)
さて、基本統計量は大きく2つに別れます。
代表値:データ全体を1つの数で表す
散布度:データのバラつきの大きさを表す
代表値の例
平均値・・・文字通り平らに均したもの。全てのバランスを保つ重心の場所を示します。
中央値・・・順番に並べた場合の真ん中になる値を指します。極端な値を避けたいときに用います。
最頻値・・・データの件数が最も頻度よく現れる値を指します。
最大値・・・データの中で最も値が大きいものを指します。
最小値・・・データの中で最も値が小さいものを指します。
散布度の例 ※基本のみ
範囲・・・データの中で上位25%-下位25%に含まれる、等の範囲に含まれる件数/比率を指します。
標準偏差/分散・・・データが平均値の周辺でどれぐらいばらついているか、を指します。偏差は平均値からの差を指します。
上記のうち、①平均値と中央値の違い、②データのばらつきを表す標準偏差/分散、をもう少し詳しく説明します。
①平均値と中央値の違い
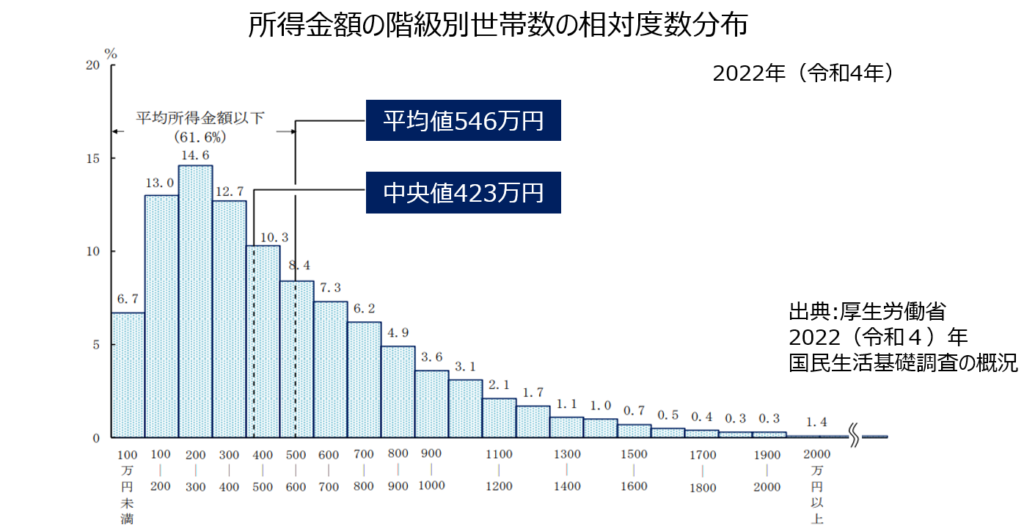
具体例を出したほうがわかりやすいので、「所得金額の階級別世帯数の相対度数分布」を見てみます。この図を見ると、平均値は546万円ですが、中央値は423万円です。なぜこのような差が出ているのかというと、平均値は、収入が極めて大きい層(1000万や2000万円以上)が大きく影響を与え、上側に引っ張られています。一方で、中央値は単純に全ての世帯を上から順に並べたときに真ん中になる値なので、極端に大きい収入の人がいても影響を受けません。このような違いがあります。(但し、統計の世界では中央値より平均値を用いる方が多いです)
②データのバラつきを表す標準偏差/分散
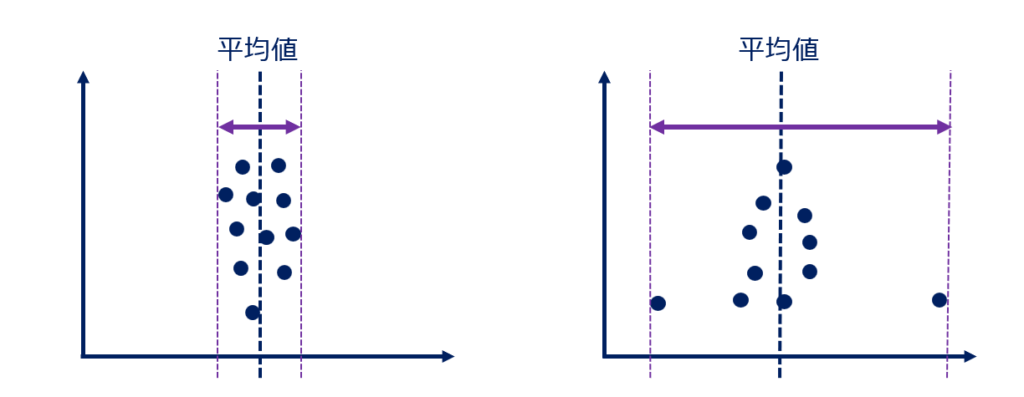
ここは2つのグラフを見比べて見ましょう。2つのグラフはどちらも平均値は同じです。しかし、点で示した各データのバラつきは異なっています。右のグラフの方がデータが平均から大きくバラついているのがわかると思います。このバラつきが分かれば各データがデータ全体の中でどの位置にいるのかがわかるようになります。例えば60点が平均値でも、50-70点の間にほとんどの人が固まっている中での80点と、20点も90点もそこそこ存在する中での80点は、意味合いが異なります。
以上、統計の基本である基本統計量に触れてみました。普段見たこと聞いたことのあるものも含まれているので、比較的馴染みやすい話題だったのではないでしょうか。





